Calculus Encoding
The generator tools in the calculus toolbox use a single JSON file, which holds the full description of a display calculus, to generate all the Isabelle and Scala code. The JSON format was chosen because it is simple to use as has parsers in many languages, including Python and Scala. Using JSON files also allows storing data easily and passing data between different systems/languages. In Python, which is used for all the code generation, importing a JSON file is a one line command:
imported_json = json.loads(json_file.read())JSON file structure
A valid calculus description file is a JSON file with these four basic key-value pairs, the structure of which is documented below:
{
"calc_name" : ...,
"calc_structure" : {
...
},
"calc_structure_rules" : {
...
},
"rules" : {
...
}
}calc_name
The value for calc_name is a string that holds the name of the calculus as it will appear in all Isabelle theories and Scala classes.
calc_structure
This section encodes the terms of the calculus, defined in Isabelle through the datatype definition.
The encoding of a type and its terms in Isabelle is transformed into the JSON file in the following way:
datatype <Term> = <Term_Constructor> <type> (<isabelle> [ [<p_1>, <p_2>,...<p_n>] <p_m> ]The generic datatype definition above is ‘disassembled’ into the JSON file below.
"<Term>" : {
"<Term_Constructor>" : {
"type" : "<type>",
"isabelle" : "<isabelle>",
"ascii" : "<ascii>",
"latex" : "<latex>",
"precedence": [ <p_1>, <p_2>,...<p_n>, <p_m> ]
}
}Note that none of the nested parameters (type, isabelle, ascii, etc.) are not compulsory and can be omitted. Further details on the parameters used by the calculus toolbox generator tools are detailed here:
| Field | JSON Data Type | Description |
|---|---|---|
| type | String | Defines the values the constructor will hold (e.g. string, int list, …) |
| isabelle | String | Defines the sugar syntax for the constructor in Isabelle (deep embedding) |
| isabelle_se | String | Defines the sugar syntax for the constructor in Isabelle (shallow embedding) |
| ascii | String | Defines the ASCII encoding, used to build the ASCII parser in Scala. If left undefined, will use the basic constructor syntax. |
| latex | String | Defines the LaTeX encoding, used to build the UI LaTeX typesetting and export functionality. If left undefined uses the basic constructor syntax. |
| precedence | Integer Array | Defines the term biding for the syntactic sugar. |
| shallow | Boolean | If defined and set to false, this attribute tells the build script that the particular constructor should not be added in the shallow embedding. For example, the free variable constructors which are needed in the deep embedding should not be added in the definition of the shallow embedding. |
| parsable | Boolean | Similar to shallow, if the value of parsable is set to false, the build script will not generate an ASCII parser for this constructor. This is useful in the definition of Sequent_Structure, for example, as this constructor is only used internally and does not constitute a valid term of the actual calculus (see here for details why it is needed). |
calc_structure_rules
All the rules of the calculus are encoded in this section of the JSON file. The rules are split up into categories both for organizational purposes and for Isabelle performance reasons (the Isabelle datatype declaration for data types with a lot of constructors take a very long time to compile). The groups for the minimal calculus, for example, include nullary (or zero-ary) and unary rule groups:
"calc_structure_rules" : {
"RuleZer" : {
"Id" : { ... },
...
},
"RuleU" : { ... },
...
}The rules themselves are encoded in the following format:
"<Rule_name>" : {
"ascii" : "<ascii>",
"latex" : "<latex>",
"condition" : "<condition>",
"locale" : "<locale>",
"premise" : "<premise>"
}| Field | JSON Data Type | Description |
|---|---|---|
| ascii | String | Defines the ASCII sugar notation, used to build the ASCII parser in Scala. If left undefined, will use Rule_name |
| latex | String | Defines the LaTeX sugar notation, used for the proof tree labels in LaTeX typesetting. If left undefined default to Rule_name |
| condition | String | This field defines any additional conditions that a rule might have. This field is directly copied into Isabelle and should be defined by valid Isabelle code (either a lambda function with the type signature Sequent ⇒ bool or a reference to a function with such type signature. This function needs to be defined in the Isabelle theory file template before the rules_rule_fun macro) |
| locale | String | If left undefined defaults to the Empty locale. The other predefined locales include CutFormula, Premise and RelAKA. |
| premise | String | Defines a custom derivation function for the premises. Must contain valid Isabelle function/reference to a defined function with the type signature Sequent ⇒ Sequent list option. For more information, have a look at the swapout rule case below. |
| se | Boolean | If set to false, the rule will not be added to the shallow embedding of the calculus. |
| se_rule | String | Overrides any definition of a rule defined in the rule section of the JSON file with the supplied string in the shallow embedding version of the calculus. Note, this string has to be a valid Isabelle term. |
rules
The encoding of the rules themselves (i.e. not just the rule name and LaTeX labels, etc.) is contained within the rules section of the JSON file. The rules follow the same format and must be grouped in the same groups as they were defined in the calc_structure_rules section:
"rules" : {
"RuleZer" : {
"Id" : ["A?p |- A?p", ... ],
...
},
"RuleU" : { ... },
...
}Instead of a dictionary, Id now has a list of Strings as its value. This list contains the ASCII encodings of the conclusion, followed by the rule premises. As mentioned in the intorduction, the $\rightarrow_L$ rule
has the corresponding JSON encoding:
"ImpR_L" : ["F?A > F?B |- ?X >> ?Y", "?X |- F?A", "?Y |- F?B"]Rule Encoding
Since proof trees are first class citizens in the DE, the inductive set definition for rules can no longer be used and explicit functions for matching sequents to rules and deriving new sequents through rule application are now defined. As detailed in the Calculi section, the match and replace/replaceAll functions match sequents with free variables (rules) to sequents that contain no free variables (concrete terms).
The application of a rule thus roughly becomes:
- the action of retrieving a rule, made up of a rule conclusion (a sequent with free variables) and the rule premises (a list of sequents with free variables)
- checking that the conclusion can be matched to the given sequent (done by the
ruleMatchfunction in Isabelle) - derivation of the premises of the rule via the match and replace/replaceAll functions.
The these steps are encoded in several separate functions that compose to create the full mechanism for sequent derivation (the der function). The rules are (roughly) encoded as pairs of sequents (conclusion) and a list of sequents (premises) in a rule function, which, given a rule will return the pair of sequents.
The der function checks the given rule conclusion is applicable to the given sequent and if it is, it will derive the premises for that sequent.
While all rules follow this general pattern, some rules, like the Cut or Swapout rules in the D.EAK calculus, will introduce some of the following restrictions/modifications to the general pattern:
- the rule can include a precondition, which has to be satisfied before a rule can be applied
- the rule can only be applied in a specific locale, i.e. it needs some extra information
- the premises of the rule are dependent on the concrete sequent and the match and replace/relaceAll functions alone cannot be used
To give these special cases in context, here are three rules which require one (or more) of these deviations from the usual pattern.
Atom
The first special rule we consider is the atom rule (formal definition given on p. 38 of the Frittella, Greco, Kurz, et al. paper on the D.EAK calculus):
Next, we introduce the structural rules which are to capture the specific behaviour of epistemic actions
Atom
$\frac{}{\displaystyle \Gamma p \vdash \Delta p} atom$
where $\Gamma$ and $\Delta$ are arbitrary finite sequences of the form $(\alpha_1) … (\alpha_n)$, such that each $(\alpha_j)$ is of the form $\{ \alpha_j \}$ or of the form, for $1 \leq j \leq n$.
Since this rule cannot successfully be matched to any sequent except for ?SX ⊢ ?SY, because $\Gamma$ and $\Delta$ can have arbitrary shape and be arbitrarily long, we need an extra precondition which can check that the given sequent is of the correct form. We can do this by defining a function atom, which recursively unfolds the structure until it either reaches $p \vdash p$ or returns false because the sequent is not of the right form:
fun atom :: "Sequent ⇒ bool" where
"atom ((Structure_Agent_Structure op1 a1 s1) ⊢ s2) = atom (s1 ⊢ s2)" |
"atom (s1 ⊢ (Structure_Agent_Structure op2 a2 s2)) = atom (s1 ⊢ s2)" |
"atom ((Atprop x)FS ⊢ (Atprop y)FS) = (x = y)" |
"atom _ = False"
| For efficiency reasons, the code in the Isabelle theory file is slightly different. However, it performs the same task. |
To add a precondition for a rule, the function of the precondition must have the following signature: (... ⇒) Sequent ⇒ bool, where ... ⇒ can be additional input parameters. However, in case the function takes additional parameters, these must be applied in the rule encoding, so that the partially applied function has a signature Sequent ⇒ bool. For example, the precondition swapin has the signature (Action ⇒ Agent ⇒ Action list) ⇒ Sequent ⇒ Sequent ⇒ bool, however in the encoding of the rule Swapin_L, the function has been partially applied: swapin rel ((BS (PhiS (?Act ''alpha'')) (;S) (AgSS (forwKS) (?Ag ''a'') (ActSS (forwAS) (?Act ''beta'') (?S ''X'')))) ⊢ (?S ''Y'')) (thust the signature of this function is Sequent ⇒ bool). |
Finally the rule itself is encoded in the following way:
"ruleRuleZer x RuleZer.Atom = ( atom ⟹C ((?S ''X'') ⊢ (?S ''Y'')) ⟹RD (λx. Some []) )"The variable x in ruleRuleZer x RuleZer.Atom ... is a variable for a locale. For more information on locales in the rule encoding, read the Cut rule case. |
This may look a bit complicated at first, but to allow for a flexible enough encoding of all the rules, some redundancy may be introduced.
For example, the code after ⟹RD, namely (λx. Some []) may seem redundant, but the reason for this encoding will perhaps be more apparent in the section on the Swapout rule.
Cut
The cut rule (single cut) is unlike most rules in the D.EAK calculus. While most rules will contain the same sub-terms in its conclusion as its premises (or will lose sub-terms going from conclusion to premises), the cut rule contains less ‘information’ in the conclusion than premises:
In the rule above, the formula $A$ no longer features in the conclusion. This fact makes proof search and derivation problematic, because while with most rules, we simply rearrange the sub-structures of a sequent (or add constants), in the cut rule, information is lost/needs to be added, depending on which direction one goes in (from from premises to conclusion or conclusion to premises). Since we go from conclusion to premises, we need to supply this information to the rule somehow.
This is where a locale comes in. A locale in the DE is a data type carrying some extra information which may be required for a successful application of a rule. In the case of the cut rule, the encoding of the rule is the following:
"ruleRuleCut (CutFormula f) SingleCut = (?S''X'' ⊢ ?S''Y'') ⟹RD (λx. Some [(?S''X'' ⊢ fS),(fS ⊢ ?S''Y'')])"| The encoding of this rule is slightly different in the Isabelle theory files. It has been adapted for better readability here. |
It should be fairly obvious to see that the cut rule can only be applied if the formula f is given.
Swapout
The swap-out rules are different to the other rules of the D.EAK calculus in that they are parametric in the given sequent (conclusion) and the $\alpha \texttt{a} \beta$ relation, as described on p. 39 of the aforementioned paper on D.EAK:
The swap-out’ rules do not have a fixed arity; they have as many premises as there are actions $\beta$ such that $\alpha \texttt{a} \beta$. In the conclusion, the symbol $\Large\textbf{;}\Big(\normalsize Y \mid \alpha \texttt{a} \beta \Big)$ refers to a string $( \ldots (Y;Y) ; \ldots ; Y)$ with $n$ occurrences of $Y$, where $n = | \{ \beta \mid \alpha \texttt{a} \beta \} |$
The rule $swap\text{-}out’_R$ given above has been formalized in Isabelle in the following way:
"ruleRuleSwapout (RelAKA rel) Swapout_R = ?S''Ylist'' ⊢ (ActSS forwAS ?Act''alpha'' (AgSS forwKS ?Ag''a'' ?S''X''))
⟹RD swapout_R rel (?S''Y'' ⊢ AgSS forwKS ?Ag''a'' (ActSS forwAS ?Act''beta'' ?S''X''))"
| The encoding of this rule is slightly different in the Isabelle theory files. It has been adapted for better readability here. |
The first part of this rule (the conclusion) looks like any other rule, but its the part after ⟹RD that differs from the standard encoding, which has the usual form (λx. Some [ ... ]). To understand what goes on in swapout_R rel (?S''Y'' ⊢ AgSS forwKS ?Ag''a'' (ActSS forwAS ?Act''beta'' ?S''X'')), let’s take a look at the signature of the function swapout_R:
fun swapout_R :: "(Action ⇒ Agent => Action list) ⇒ Sequent ⇒ Sequent ⇒ Sequent list option" where ...Without going into details of what swapout_R does, notice that the partially applied function swapout_R rel (?S''Y'' ⊢ AgSS forwKS ?Ag''a'' (ActSS forwAS ?Act''beta'' ?S''X'')) will have the type signature Sequent ⇒ Sequent list option, which corresponds to the lambda function (λx. Some [ ... ]) (where ... is a list of sequents).
One can see that this function takes a sequent and either succeeds in deriving the premises (returns a Some (Sequent list)) or fails and returns None. In this rule, the swapout_R function supersedes the match and replace/replaceAll functions and is used instead, however match and replace/replaceAll are automatically used for all the other rules where they are sufficient. For details on how this works, have a look at the der function in the Calc_Rules.thy template.
Rule Macro
The macro ‘rule’ is a special rule that gets added to any generated calculus by default. The motivation for the macro rule arises from the notion of derived rules in a calculus. Since derived rules can be used quite frequently, the Scala UI provides an easy way to create macros that can be applied in a similar fashion to the defined rules of the calculus. These macros represent snippets of proof tree skeletons where the sequents contain free variables to be substituted for by concrete terms, when applied.
In Isabelle, datatype Rules is mutually dependent on the datatype Prooftree, as a result of the definition of RuleMacro:
datatype Rule = RuleZer RuleZer
.
.
.
| RuleMacro string Prooftree
| Fail
and Prooftree = Prooftree Sequent Rule "Prooftree list" ("_ ⟸ PT ( _ ) _" [341,341] 350)Due to the nature of the UI tools (namely that the proof tree generated by the tools must always be valid), these derived proof tree snippets have concrete terms substituted in, are checked for validity and added directly to the main proof tree. To remove clutter, the snippet of the proof tree is stored separate from the main proof tree structure. To demonstrate, let’s take a look at a derived rule in the D.EAK calculus, $W_R$:
Here X, Y and Z are variables that can be substituted by concrete terms. Often, the full proof tree won’t be written out and only the derived rule name label would be added to indicate that a derived rule was used:
| $\frac{\displaystyle \frac {\displaystyle \frac{}{p \vdash p}} {p > p \vdash q} } {\displaystyle \frac {p \vdash p ; q} {\vdots} }$ | $\Large\Rightarrow$ | $\frac{\displaystyle \frac{}{p \vdash p}} {\frac{\displaystyle p \vdash p ; q} {\displaystyle \vdots}} W_R$ |
The use of rule macro simulates this in the Scala UI, keeping the proof trees shorter and more readable:
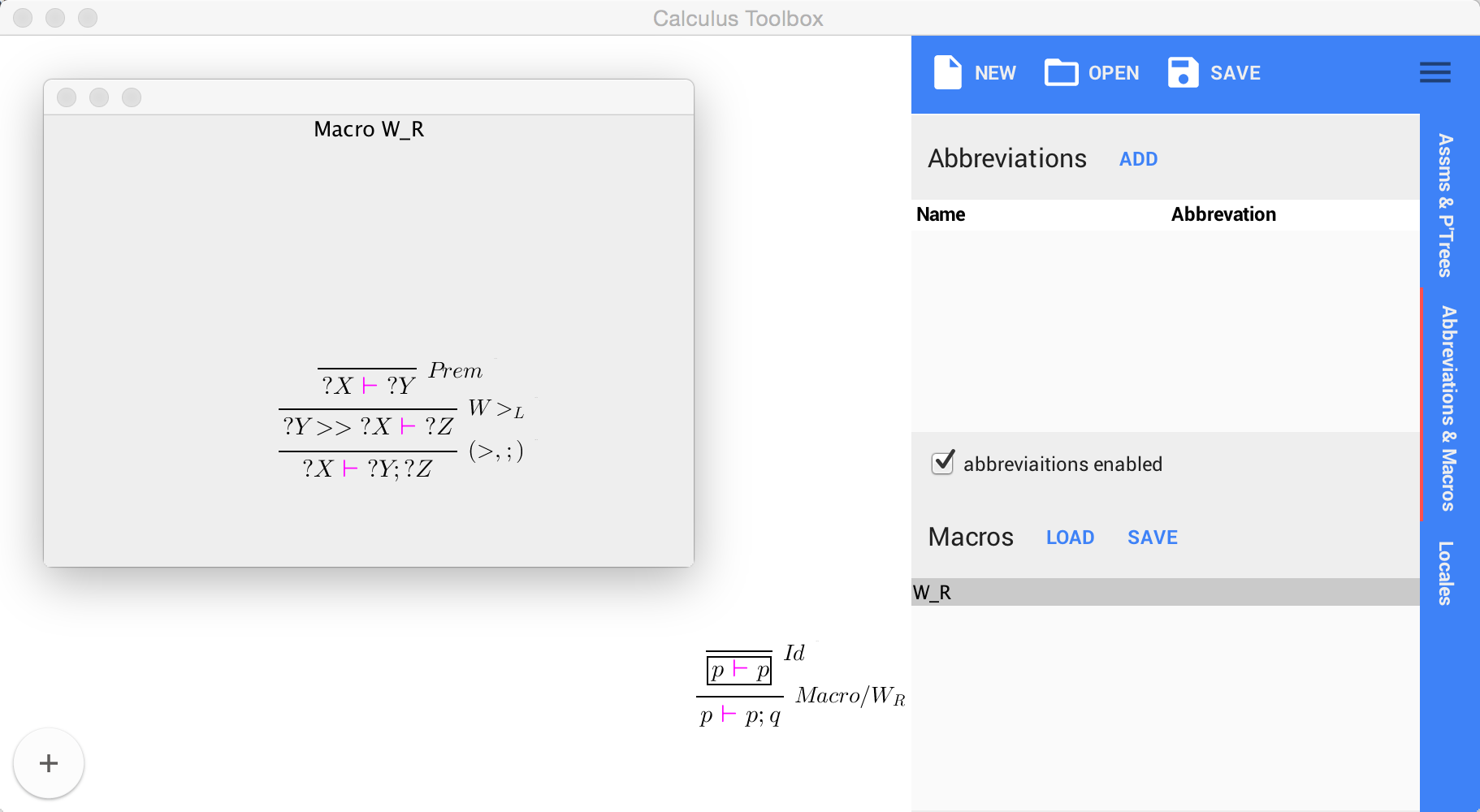
At the same time, the underlying encoding (ASCII and Isabelle) carries the macro proof tree within the the main proof tree, and this means that the main proof tree can be checked for validity without relying on any external definitions of derived rules. To learn how to define and use rule macros, have a look at the Scala UI documentation.