Scala UI
UI Overview
After generating the calculus and recompiling all the UI classes, running make gui inside the generated calculus should produce the window below.
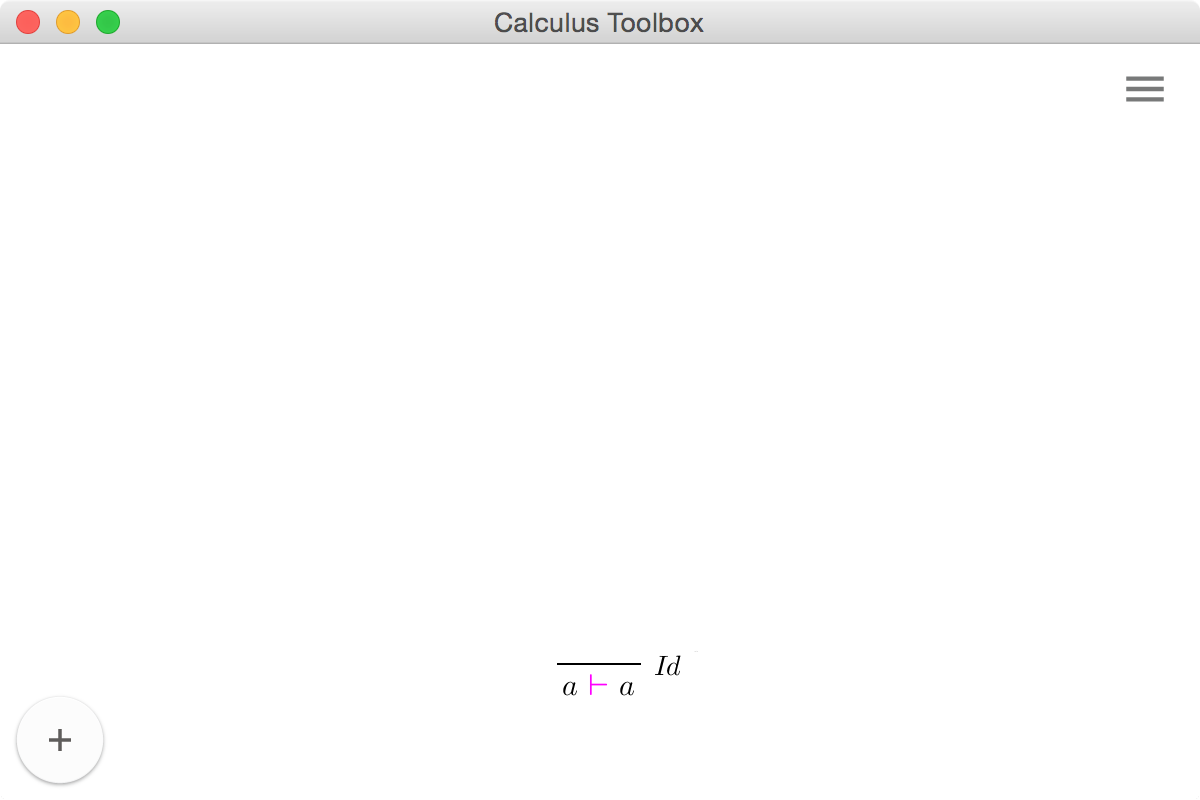
The + button in the bottom left corner of the window opens up a bar containing a text input field, used by the user to input sequents into the UI. The user uses ASCII and if the input can be parsed, it is typeset in LaTeX for better readability. Pressing Enter after the user entered a valid sequent will launch the proof search. If the proof search is successful, the resulting proof tree found is displayed in the panel below. The UI allows the user to interactively modify the proof trees by clicking on any of the sequents in the tree:
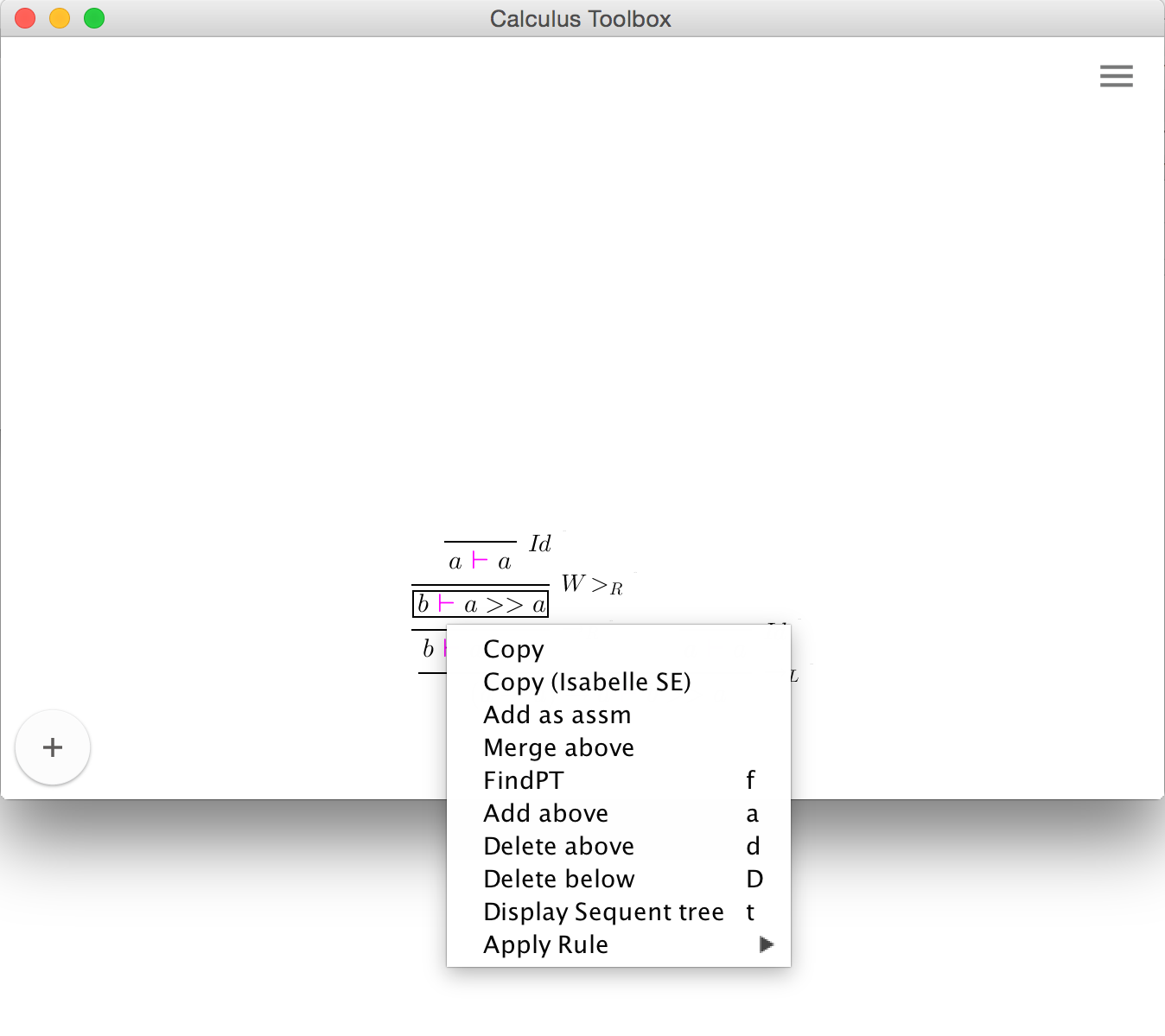
Each sequent in the proof tree can be clicked on and the proof tree can be modified at this point. The options, listed in the drop down menu shown above, are described in more detail in the following table:
| Copy | Copies the selected sequent as an ASCII string |
| Add as assm | Adds the selected sequent to the list of assumptions |
| Merge above | Looks at all the generated proof trees in the session (shown in a list on the right), searching for a proof tree with a conclusion which matches the selected sequent. If such a proof tree is found, it is copied into the current one and merged at the selected sequent. Note that the selected sequent must be a leaf of the tree. (To make the selected sequent a leaf, use the option Delete above) |
| FindPT | This option will start a proof search with the selected sequent as the goal/target. If a proof tree is found, it is automatically added into the current proof tree. |
| Add above | If the selected sequent is a leaf in the proof tree, add above will open a dialog window with a list of all applicable rules for the selected sequent: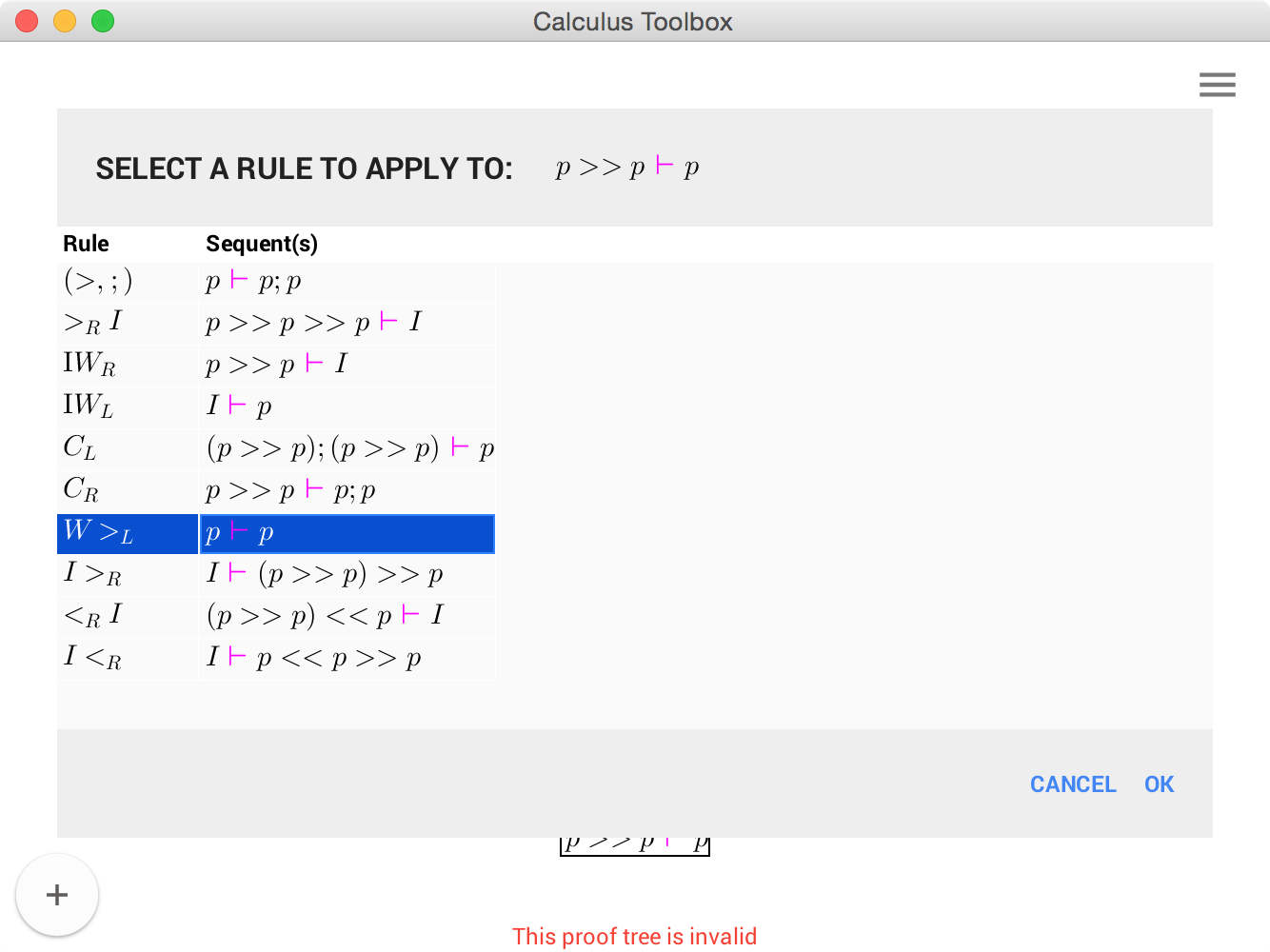 Selecting a rule form the list will apply the rule to the selected sequent and derive the premises, adding them to the tree. |
| Add below | If the selected sequent is at the root of the tree, this option will allow the user to grow the tree downwards, i.e. to generate a proof tree for a different conclusion by extending the current proof tree downwards. A prompt for the new conclusion will be displayed, and if a rule is found that can derive the current conclusion from the new one, the new conclusion will be added as the root of the tree. |
| Delete above | Delete above simply removes any part of the proof tree above the current sequent and turns the current sequent into a premise |
| Delete below | Delete below removes any part of the proof tree below the current sequent, making the current sequent the root/conclusion of the proof tree |
| Apply Rule | This menu unfolds into a sub-menu of rule tactics or special rules that require further user input such as the cut rule (if cut is defined in the calculus) |
Next in main screen is the sidebar icon in the top right corner. When clicked, the sidebar is presented to the user. This sidebar contains all the assumptions and proof trees in this session as well as the loaded up macros, abbreviations and locales(split up in tabs along the right side of the sidebar). The proof trees and assumptions can be saved into a text file and loaded back up into the UI (Use the OPEN and SAVE icons in the sidebar).
To add a sequent as an assumption, first type the sequent into the text input at the top and when the sequent is parsed, click on the Add assm button underneath the assumption list.
|
In order to use assumptions in the and to Lastly, type |
The proof tree list holds all the added proof trees. To switch between them, simply double click on a proof tree in the list (the list labels are the conclusion sequents of each proof tree). Right clicking on an individual proof tree brings up the following drop-down menu:
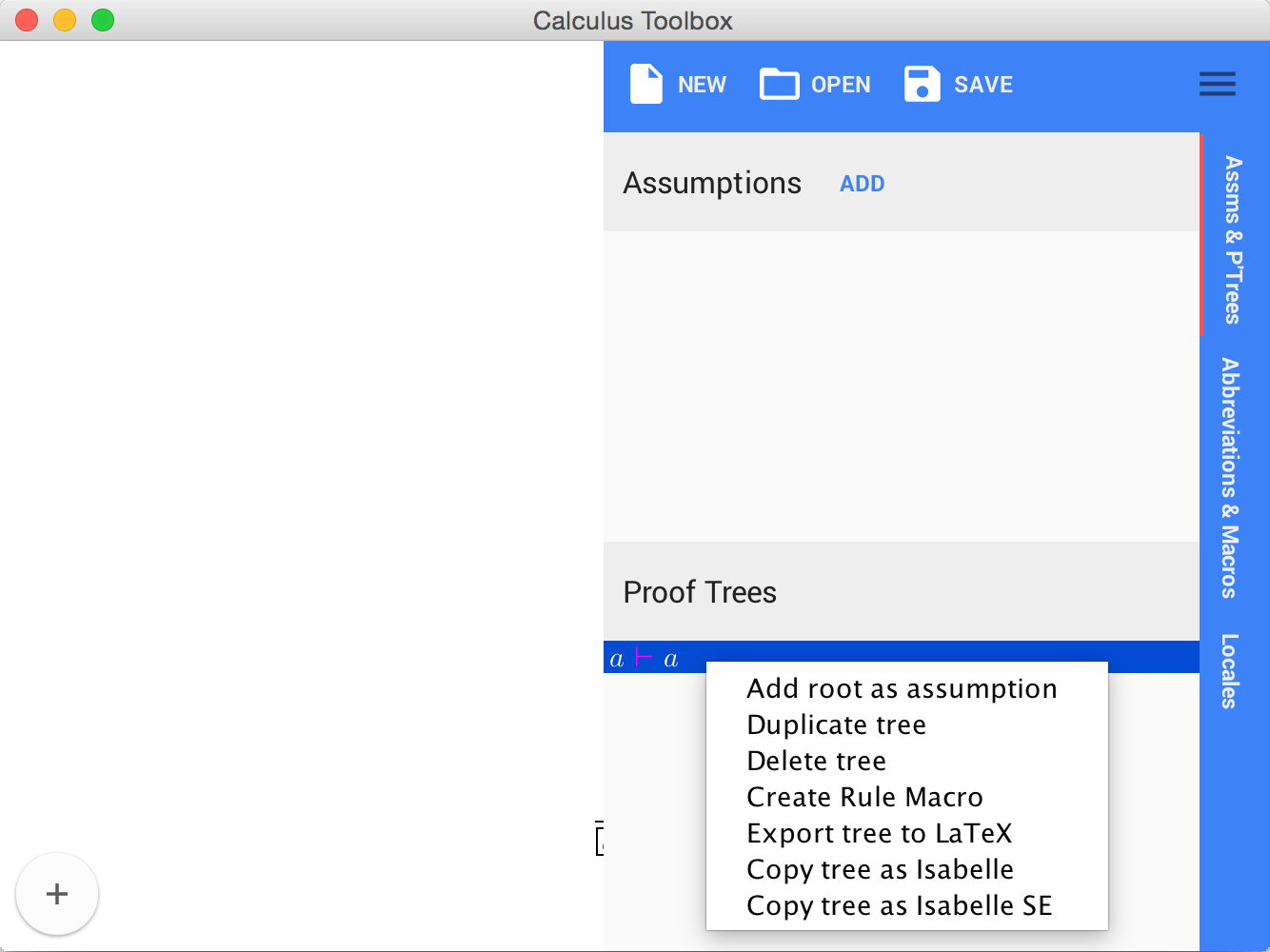
| Add root as assumption | Adds the root sequent of the selected proof tree to the list of assumptions |
| Duplicate | Duplicates the selected proof tree |
| Delete | Deletes the selected proof tree (you can also delete a proof tree/list of proof trees by highlighting and pressing the Delete key on the keyboard ) |
| Export to LaTeX | Prompts the user to select a file name and then exports the selected proof tree to latex (the proof tree type setting requires bussproofs.sty) |
| Copy tree as Isabelle (SE) | Copies the entire proof tree into the clipboard (as a string). This proof tree can be pasted into an Isabelle theory file. |
| Create Rule Macro | Creates a macro form the selected proof tree. For more information, read the section on locales. |
The next tab of the sidebar holds the user defined abbreviations and macros. In this tab, the user can load, view, manage and save macro rules. The user can also define abbreviations, which allow the hiding of more complex formulas or structures under a single identifier, as seen below, where an abbreviation $x$ for the formula $a \vee b$ was added. Abbreviations can be toggled by the “abbreviations enabled” check-box.
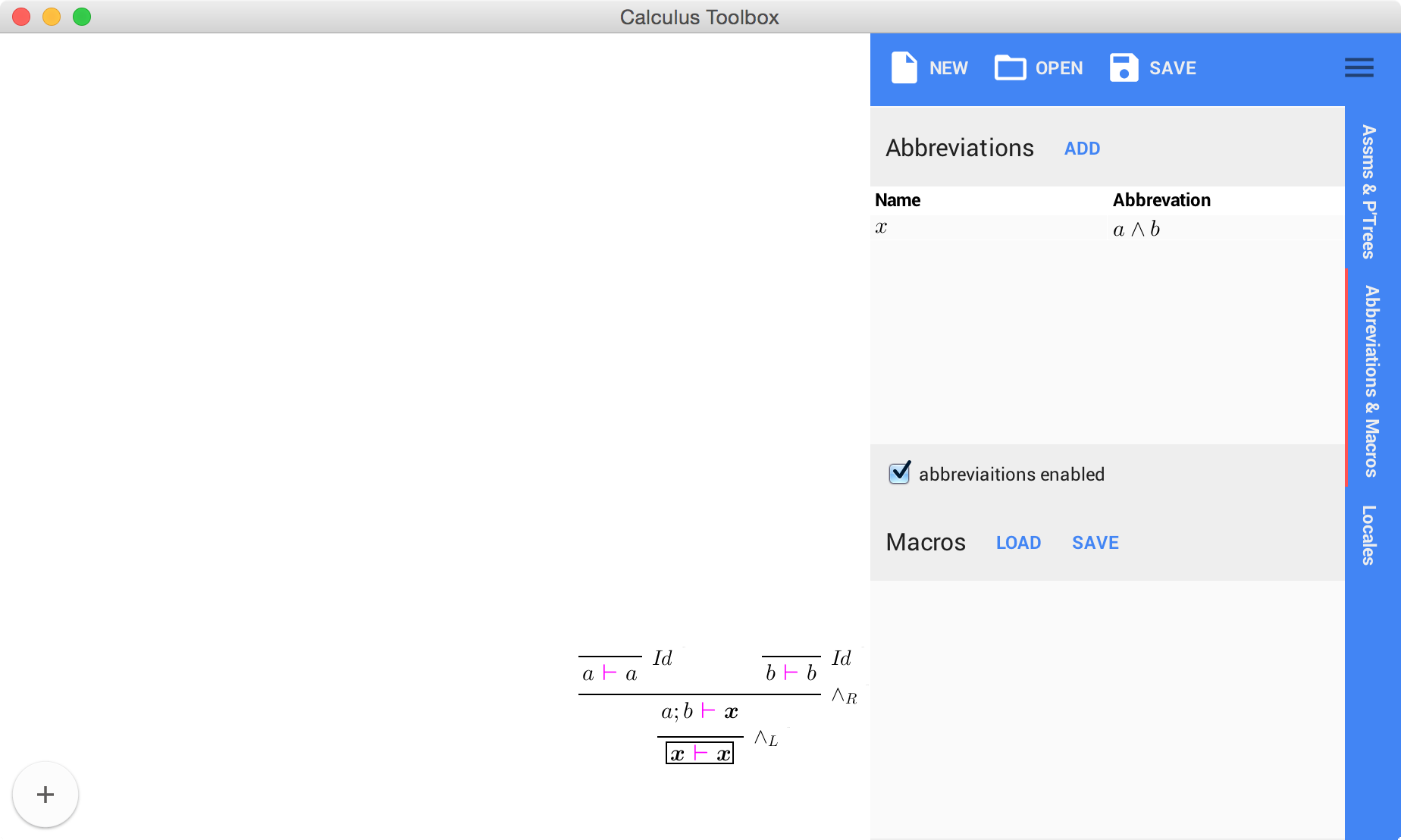Note that the abbreviations are stored in the same file along with the proof trees, assumptions,and any user defined locales.
The last tab contains the definition of locales, detailed in a separate section of this document.
LaTeX Typesetting
A big motivation for the UI tools was the difficult readability of the encoded calculus. The full D.EAK calculus, even with syntactic sugar, is already quite far removed form the LaTeX representation, however the real trouble comes with the encoding of the proof trees.
For demonstration, this is an encoding of a proof tree in Isabelle:
(Atprop ''p'' F S ⊢S BS Atprop ''p'' F S ;S Atprop ''q'' F S) ⟸ PT RuleDisp ImpR_comma_disp2 [(BS Atprop ''p'' F S →S Atprop ''p'' F S ⊢S Atprop ''q'' F S) ⟸ PT RuleStruct W_impR_L [(Atprop ''p'' F S ⊢S Atprop ''p'' F S) ⟸ PT RuleZer RuleZer.Id []]]
Even after formatting and lining up the code snippet above, the coding is still quite hard to read:
(Atprop ''p'' F S ⊢S BS Atprop ''p'' F S ;S Atprop ''q'' F S) ⟸ PT RuleDisp ImpR_comma_disp2
[(BS Atprop ''p'' F S →S Atprop ''p'' F S ⊢S Atprop ''q'' F S) ⟸ PT RuleStruct W_impR_L
[(Atprop ''p'' F S ⊢S Atprop ''p'' F S) ⟸ PT RuleZer RuleZer.Id []]]
When typeset in LaTeX however, the proof is readable immediately:
Due to this, the UI was initially developed with the express intention of pretty printing the proof trees generated by the proof search algorithm. The reasons Scala was used for the UI were twofold. The main reason Scala was chosen was due to the fact that the code export tool in Isabelle supported exporting code to Scala. The second reason, tied to the need for a UI and LaTeX typesetting, was the ability of Scala to import and use Java libraries.
The library used for LaTeX typesetting of the calculus terms is JLaTeXMath. The library includes a subset of the available LaTeX packages and has so far been sufficient for all typesetting. The advantage of the library is the complete independence of the system version of LaTeX, as it is self contained. However, this library does not contain the bussproofs.sty style sheet. This meant that the proof trees inside the UI had to be laid out without the use of LaTeX. Another library, TreeLayout, was used to layout the individual sequents into a proof tree in the UI. This approach, whilst more complicated than using LaTeX typesetting of the full proof trees, allowed for the easy addition of interactivity to the proof trees by adding context menus, as seen in the section above.
Proof search
The proof search algorithm was initially implemented in Haskell and later migrated to Scala. Since both Haskell and Scala are functional programming languages, the proof search algorithm is extremely short, the core method body is only about 10 lines of code:
def derTrees(loc:List[Locale], n:Int, seq:Sequent):Option[Prooftree] = n match {
case 0 => None
case n =>
for((rule, derList)<-derAll(loc, seq).sortWith(_._2.length < _._2.length)) {
lazy val ders = derList.map(x => derTrees(loc, n-1, x))
if(!ders.contains(None))
return Some(Prooftreea(seq, rule, ders.map{case Some(pt) => pt}))
}
return None
}Since the algorithm is very short, it will come as no surprise that it is quite a simple one. The function above simply gets a list of possible rules it can apply and it will recursively do so until reaching a premise or ‘timing out’. The integer n in the method declaration is used as a counter to guarantee termination. If the counter reaches zero before a premise or a nullary rule is derived, the function will terminate with an unsuccessful result, the empty list. If a nullary rule or a premise is reached before this point, the search terminates and the found proof tree is added to the list.
The proof search in its current form is useful for finding proof trees with about 5 levels. As the time complexity is exponential with search depth, the algorithm isn’t feasible beyond the depth of 7. An auxiliary function is used to search for proof trees of ascending depth until a proof tree is found or the maximum depth is reached.
The proof search functionality has much potential for improvement, mainly in reducing the search space for valid proof trees by a more directed search (one improvement might be taking reversible rules into consideration and disregarding the application of their reverse immediately succeeding said rule application, by keeping the history of applied rules in memory).
Locales
A locale in the calculus toolbox is a special data type which carries extra information for rule derivation. The need for locales arises from the D.EAK calculus rules, some of which contain side conditions and rely on extra information for successful application (these are detailed in the Calculus Encoding section).
The locales in the toolbox are somewhat similar to Isabelle’s locales, which create an enclosed ‘environment’, where certain assumptions and conditions hold. This is the case for some proofs in the calculus, which are only valid under certain assumptions. The isProofTree function therefore requires a list of locales, which it tries to use to successfully derive all the sequents of the proof tree in sequence. If a locale needed for a certain rule is missing, the proof tree will not be valid. Since the locales are user defined, the UI provides facilities for defining some of them. The current toolbox contains the following locales:
CutFormula
This locale carries a formula which is used for the application of the cut rule. To apply cut in the UI, the user selects the ApplyCut option when clicking on a sequent within a proof tree. The user is prompted to enter a cut formula, which is stored inside a CutFormulalocale and used in the der function when applying the cut rule.
The CutFormula locale is needed for proof search (if the proof search is allowed to use the cut rule), when growing the tree from the root to the premises. However, the isProofTree function does not require the cut formulas found in the proof tree to be supplied in the list of locales, because it is easy to collect the cut formulas from the given proof tree (even if we do not know if it is valid beforehand). The collectCutFormulas function (found in Calc_Rules.thy) traverses the given proof tree and collects the cut formula at any level where the cut rule is applied (rather where the cut rule label is found). The cut formula is the formula, which is both the antecedent one premise and at the same time the consequent of the other one, as is clear from the rule itself:
Once the cut rules have been collected into the locale list, the isProofTree then recursively applies der function, checking that the derivations at level are correct.
Premise
The premise locale has been introduced to allow user added premises. This can be especially useful in proof search, as the user can add sequents that are not axioms to the proof search, allowing a guided search which terminates at the user defined premise. The list of current premises can be found in the sidebar of the Scala UI, and premises can be added in several different ways, as documented in the sections above.
| Similarity to the CutRule locale, the premises in a concrete proof tree are collected by the collectPremises function when isProofTree is applied. This means that the premises act as axioms even though they may not actually be valid. |
Empty
This is the base locale, added to the list of locales by default. Since a locale must always be supplied to the der function, the empty locale signifies a locale with no extra information or assumptions. Since most rules of the minimal and the D.EAK calculus do not require locales, the rules can be applied with any given locale, including but not limited to the empty locale.
RelAKA
The relAKA locale is specific to the Swapin and Swapout rules in the D.EAK calculus. These rules can only be applied in specific circumstances, or rather, only under under a certain relation of the current sequent’s sub-terms (more specifically, it is a relation between an Action, Agent and a list of Actions).
To define a relAKA in the UI, open up the sidebar and switch to the Locales tab. The definition of relAKA is found under the Action structure section of the sidebar. By clicking on the ADD button, the user is prompted to enter the Action, Agent, Action triple.
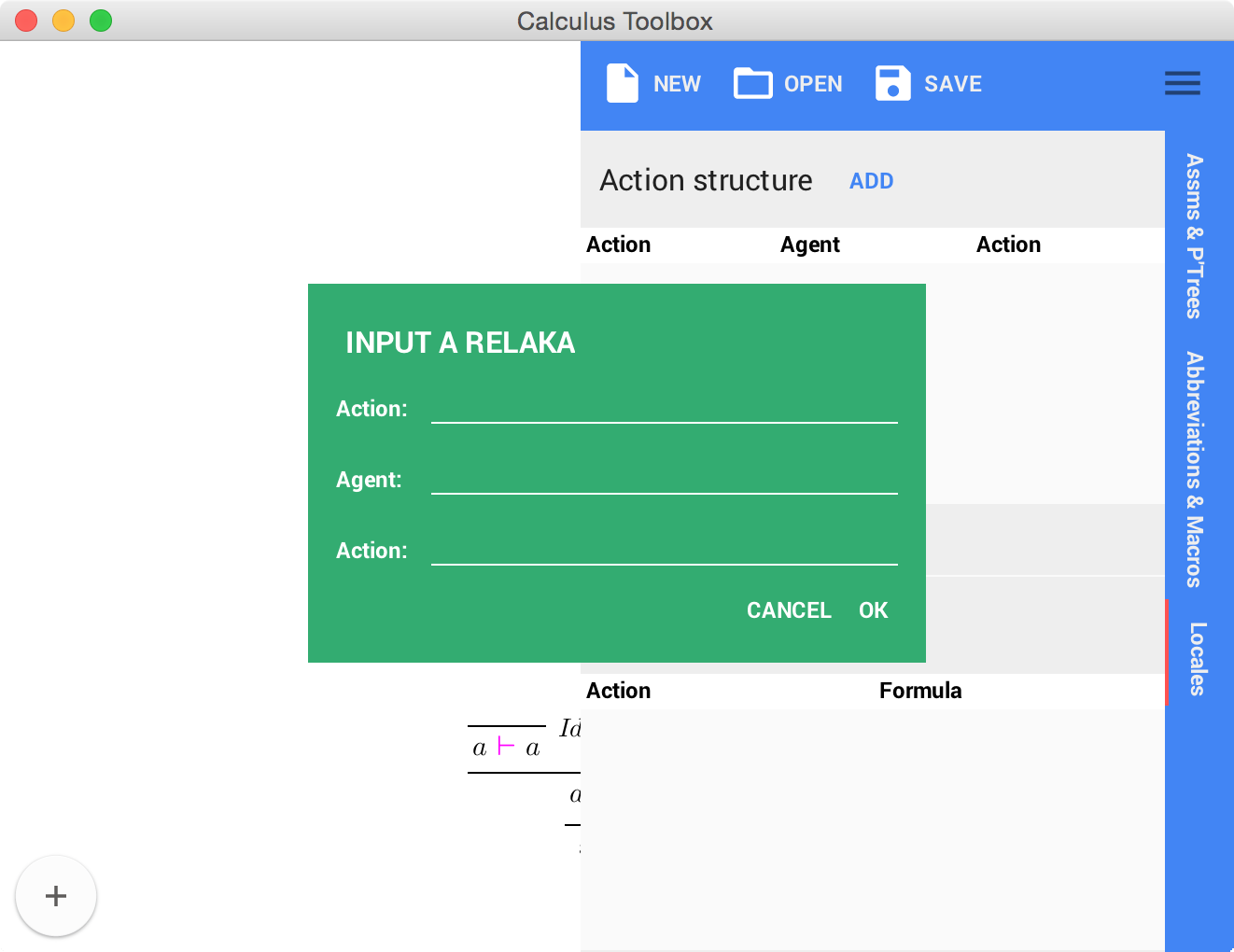
| Note that any proof trees which rely on a specific relAKA will only be valid if said relAKA is currently loaded in the UI |
PreForm
The preForm locale is a map between actions and their corresponding preconditions (formulas). This locale is needed when applying the $Pre_L$ or $Pre_R$ rules, which substitute an action for its corresponding precondition.